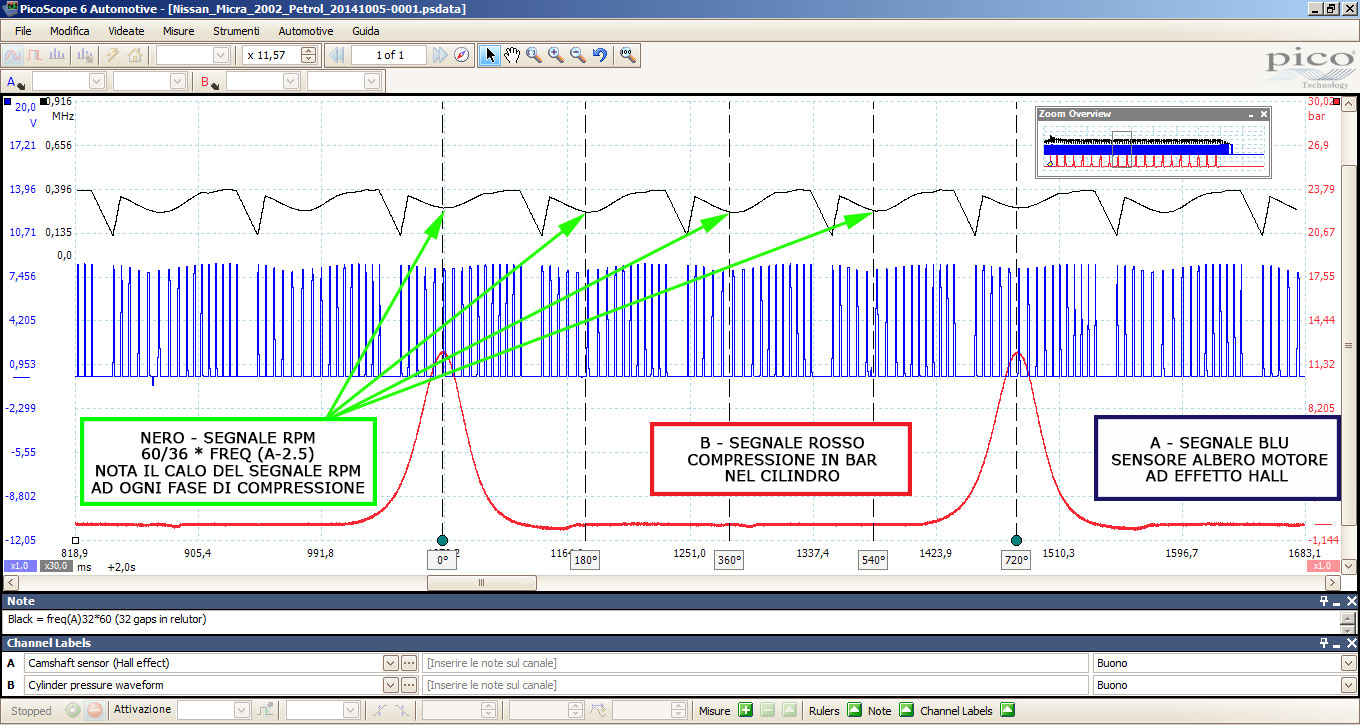
Calcolo matematico per visualizzare curva Rpm

Lo sapevate che si possono utilizzare le funzioni dei canali matematici per calcolare e visualizzare graficamente una curva RPM (giri al minuto)? Questa funzione potrebbe essere veramente utile quando si cercano dei misfire in piccole variazioni della velocità motore.

Per visualizzarla nel PicoScope dobbiamo creare la formula matematica del canale per calcolare la frequenza del nostro segnale velocità motore relativo a 1 giro dell'albero motore e moltiplicarlo per 60.

Esempio. La ruota dell’albero motore ha 36 denti con 2 mancanti come TDC (punto morto superiore) di riferimento. Mentre in realtà abbiamo 34 denti, dobbiamo includere i denti mancanti nella nostra formula per ottenere risultati accurati su RPM. Per spiegare ulteriormente come la funzione dei canali matematici sono in grado di visualizzare la curva RPM abbiamo bisogno di tornare alla teoria.

Stiamo esaminando la frequenza (misurata in Hz), ma abbiamo bisogno di giri al minuto (RPM):

RPM = Frequenza (Hz) x 60 (in riferimento al numero al minuto, quindi 60 secondi in un minuto)

Quindi: 1 la rotazione di 36 denti sulla ruota del nostro albero motore è pari a: Hz x 60
La formula matematica canale è scritto come segue: 60/36 * freq (A-2.5)

Ciò consente al PicoScope di calcolare la curva RPM basata sui 36 denti del segnale di velocità del motore.

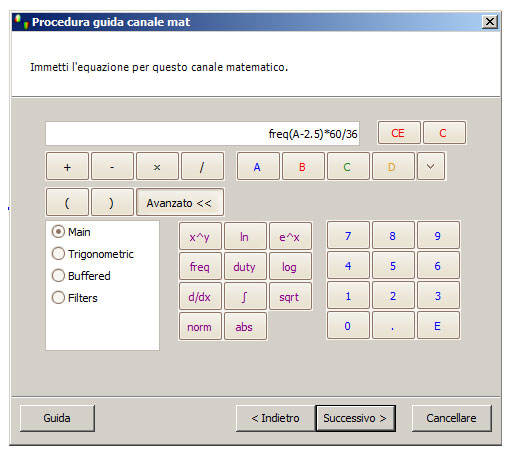
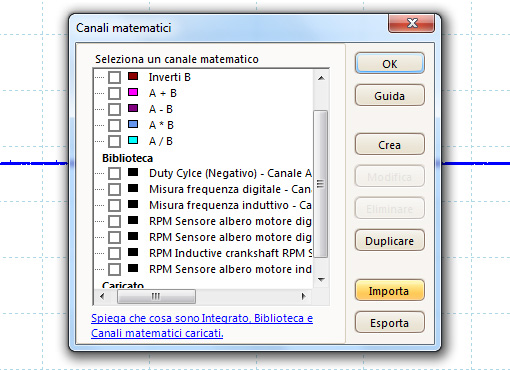
1. Selezionare Strumenti> Canali matematici e poi Crea.
2. Fare clic su Avanzate
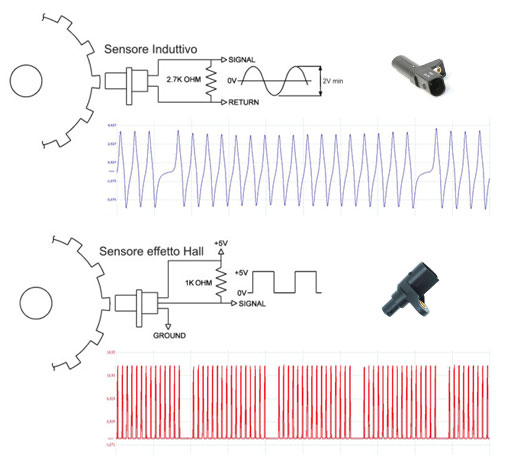
3. Inserire "60/36 *" e quindi il pulsante freq. Quando freq () appare nella casella Tipo formula "A 2.5" se abbiamo un sensore ad effetto Hall di giri del motore sul canale A o semplicemente "A" per un sensore di velocità del motore induttivo.
a. Tutta la formula sarà simile a 60/36 * freq (A-2.5) per i sensori digitali e 60/36 * freq (A) per sensori induttivi (entrambi con 36 denti, in realtà 34, come due sono mancanti).
4. Fare clic su Avanti. Scegliere qualsiasi colore che preferisci per il tuo canale matematica RPM.
5. Fare clic su Avanti.
a. Nella parte superiore (unità) sezione tipo "Speed Engine" nel nome lungo e "RPM" nel nome breve.
b. Nella sezione Intervallo è meglio attivare Ignora selezione automatica del campo. Questo consente di intervento manuale per la gamma attuale si richiede (nell'esempio ho selezionato 0 RPM a 1500 RPM).
c. Fare clic su Avanti e Fine.
d. Tramite il menu contestuale (clic destro del mouse) abilitare il creato Maths Channel e fare clic su OK.

Apparirà il tuo nuovo canale matematico e sarà in grado di tracciare il numero di giri del canale che si è richiesto (nel nostro caso A-2.5 è un canale matematica RPM per Canale A).

Le formule matematiche tipiche per diverse configurazioni di velocità del motore sono:

- Sensore digitale con 36 denti sul canale A = 60/36 * freq (A-2.5)
- Sensore induttivo con 36 denti sul canale A = 60/36 * freq (A)
- Sensore digitale con 60 denti sul canale A = 60/60 * freq (A-2.5)
- Sensore induttivo con 60 denti sul canale A = 60/60 * freq (A)

Ovviamente i calcoli matematici sui canali non si limitano al segnale del sensore albero motore. Ogni segnale stabile in uscita che fa riferimento ad 1 giro completo albero motore può essere utilizzato come riferimento. Ad esempio le pulsazioni in pressione sul gas di scarico su un motore 4 cilindri:
2 x pulsazioni dei gas di scarico per giro dell'albero motore possono essere utilizzate per ottenere la curva RPM (giri motore), nella formula 60/2 * freq (A)

Con un po’ di esperienza si possono effettuare infinite misurazioni e si aprirà un nuovo mondo di tecniche di diagnosi avanzate e molte nuove informazioni su un singolo segnale campionato.

Scarica un pacchetto ZIP con i canali matematici in italiano

- Duty Cycle (Negativo) - Canale A.psmaths
- Misura frequenza digitale - Canale A.psmaths
- Misura frequenza induttivo - Canale A.psmaths
- RPM Sensore albero motore digitale 36 denti - Canale A.psmaths
- RPM Sensore albero motore digitale 60 denti - Canale A.psmaths
- RPM Sensore albero motore induttivo 36 denti - Canale A.psmaths
- RPM Sensore albero motore induttivo 60 denti - Canale A.psmaths

Download cartella zip

Nota tecnica:

Un canale matematico è una funzione matematica di uno o più segnali di ingresso. La funzione può essere semplice come "Inverti A", che sostituisce il pulsante Inverti su un oscilloscopio convenzionale oppure una funzione complessa definita dall'utente. Può essere visualizzato in un una vista oscilloscopio, XY o spettro come un segnale in ingresso, e come un segnale in ingresso ha il proprio asse di misurazione, il pulsante di dimensionamento in scala e compensazione e colore. PicoScope 6 dispone di una serie di canali matematici incorporati per le funzioni principali, tra cui "A+B" (la somma dei canali A + B) e "A-B" (la differenza tra i canali A e B). È inoltre possibile definire le proprie funzioni mediante l'editor di equazioni o caricare canali matematici predefiniti da file.

Approfondimenti consigliati:

        Funzione canali matematici su PicoScope (cap 5.21)

        Download file con curva RPM Nissan Micra 2002

Torna al Software